Em nosso dia-a-dia estamos sempre comparando e relacionando números, grandezas e formas. Antes mesmo de contar, o homem primitivo já tinha essas noções.
- Número: diferenciava uma de muitos.
- Grandeza: diferenciava pequeno de grande.
- Forma: diferenciava redondo de retilínio. A forma redonda da Lua e a ponta retilínea de uma rocha.
Até mesmo uma criança, antes de dominar a fala, também já possui essas noções.
Basicamente, uma função é a relação entre duas coisas na qual o valor numérico de uma coisa em alguma forma depende do valor da outra:

- A temperatura diária média para a sua cidade depende,e
é uma função de,
da época do ano.
- A distância que um objeto caiu é uma função de quanto tempo passou desde que você o soltou;
- A área de um círculo é uma função do seu raio;
- Número de pães que vou comprar, com o preço a pagar;
- Velocidade média do automóvel, com o tempo de duração de uma viagem.
"As Características Explicativas de uma Função". Um função tem apenas um valor de saída (output) para um valort de entrada (input).

 O que é uma função?
O que é uma função? A máquina de refrigerante é uma função porque depois de inserir os dados de entrada (sua escolha e seu dinheiro), você sabe exatamente qual é o retorno. Com a máquina caça-níqueis, por outro lado, o output é um mistério,então não é uma função.
O conjunto de todos os inputs é chamado de domínio; o conjunto de todos os outputs é é chamado de imagem. NOTAÇÃO DE FUNÇÃO NUMÉRICA:
Com os conjuntos A={1, 4, 7} e B={1, 4, 6, 7, 8, 9, 12} criamos a função f: A —> B.definida por f(x) = x + 5 que também pode ser representada por y = x + 5. A representação, utilizando conjuntos, desta função, é:
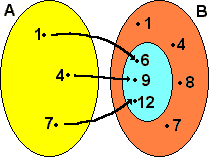
O conjunto A é o conjunto de saída e o B é o conjunto de chegada (ignore o conjunto azul por enquanto).
Domínio é um sinônimo para conjunto de saída, ou seja, para esta função o domínio é o próprio conjunto A = {1, 4, 7}.
Como, em uma função, o conjunto de saída (domínio) deve ter todos os seus elementos relacionados (regra 2 das funções), não precisamos ter subdivisões para o domínio.
O domínio de uma função também é chamado de campo de definição ou campo de existência da função, e é representado pela letra "D".
O conjunto de chegada "B", também possui um sinônimo, é chamado de contradomínio.
Note que podemos fazer uma subdivisão dentro do contradomínio (conjunto azul da figura acima). Podemos ter elementos do contradomínio que não são relacionados com algum elemento do Domínio e outros que são. Por isso, devemos levar em consideração esta subdivisão (esta é até mais importante do que o próprio contradomínio).
Este subconjunto é chamado de conjunto imagem, e é composto por todos os elementos em que as flechas de relacionamento chegam.
O conjunto Imagem é representado por "Im", e cada ponto que a flecha chega é chamado de imagem.
*Obs.: Note que existe uma diferença entre imagem e conjunto imagem, o primeiro é um ponto em que a flecha de relacionamento toca, e o segundo é o conjunto de todos elementos que as flechas tocam.
No nosso exemplo, o domínio é D = {1, 4, 7}, o contra-domínio é = {1, 4, 6, 7, 8, 9, 12} e o conjunto imagem é Im = {6, 9, 12} e:
- a imagem do ponto x = 1 é y = 6, indicado por f(1) = 6;
- a imagem do ponto x = 4 é y = 9, indicado por f(4) = 9;
- a imagem do ponto x = 7 é y = 12, indicado por f(7) = 12.
Fonte:www.tutorbrasil.com.br/estudo_matematica_online/funcoes/funcao_geral/funcoes_03_01.php
Acessar o Link "abaixo":
http://www.youtube.com/watch?v=0Sj7UFbQEVY&feature=youtu.beComente: O que é uma função?
Um forte abraço
Prof Renata S





















.jpg)
.jpg)
.jpg)
.jpg)















