Este blog foi feito pra você... Que fica com cara de ué, nas aulas de matemática!!!!
30 de abril de 2012
A Geometria do Dia-a-Dia: 2º Ano - Ensino Médio.
Olá Queridos Alunos.
Neste domingo estive no supermercado, e como todo "boa" Dona de Casa, comprei detergente para lavar louças, sempre compro da marca Ypê, para minha surpresa a ambalagem mudou! Logo, me questionei: Mudou porque? Se o formado continua sendo um cilindro, entretanto de altura menor que a embalagens anterior, e de área da base maior que a anterior de também! Agora, precisamos saber o que motivou da empresa há essa mudança, sendo que as duas embalagens têm a mesma capacidade (volume). Logo precisamos calcular a área da superfície das duas embalagens (ver imagem).
- Embalagem de altura maior: Diâmetro igual a 5,3 cm e altura igual aproximada 23,5 cm.
- Embalagem de altura menor: Diâmetro igual a 6 cm e altura igual 21 cm.
Qual a área da Superfície de cada embalagem?
Estava em um aniversário de uma amiga, quando me deparei com os enfeites das mesas, fiquei pensando quanta geometria em um simples enfeite...
Observem: São três esferas de mesmo volume; três cilíndros (base de sustentação das esferas) e um tronco de uma pirâmide! Eu sei que vocês estão ansiosos para calcular, entretanto aguardem: logo, logo... vou postar as medidas...
Um Forte Abraço
Prof Renata
22 de abril de 2012
Numeros Complexos: 3º ano - Ensino Médio.
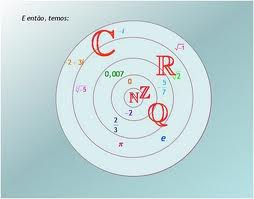
Olá Queridos Alunos
O surgimento dos números complexos constum se relacionado, erroneamente, às resoluções de equações 2º grau, nas quais se encontram raízes quadradas de números negativos. As equaçõesdo 2º grau surgiram há tempos na Matemática (cerca de 1700 a.C.), e o aparecimento da raízes quadradas de números negativos nas resoluçõs nunca foi um problema para os matemáticos. Isso porque as equações eram formuladas a fim de se obter uma solução para um problema concreto e, se aparecessem ráizes negativas, concluía-se simplesmente que o problema não tinha solução. O observe abaixo o surgimento dos números complexos que está relacionado com as resoluções de equações do 3º grau, em que aparecem raízes de numéros negativos:
Niccolo Tartaglia (cerca de 1500-1557)


Gerônimo Cardano (1501-1576)


Raphale Bombelli (cerca de 1526-1573)


Leonard Euler (1707-1783)


Carl Friederich Gauss (1777-1855)

A existência de um novo tipo de número foi de difícil aceitação, mas, com tempo, diversos matemáticos trabaram com esses números. Seu maior desenvolvimento somente se deu após a descoberta de aplicações em outras áreas.
Assistam o vídeo e façam e estudem a apostila 10, e caso seja possível resolva os exercícios.
Um Forte Abraço.
Prof Renata S
Apostila 2: Função do Segundo Grau - 1º ano do Ensino Médio.
Olá Queridos Alunos.
O estudo da Função Quadrática, é muito parecido com os conceitos e aplicações da Função Afim, entretanto o comportamento da Função Quadrática e diferente da Função Afim, é justamente isso que vamos estudar:
O gráfico da função quadrática corresponde a uma curva muito especial em Matemática chamada parábola. A parábola é uma curva do plano cujos pontos satisfazem uma condição bem definida.
Assistam os vídeos, vejam as aplicações bem como a forma geral de representar uma função quadrática, e faça um estudo comparativo utilizando a Apostila 2:
Um Forte Abraço
Prof Renata S
O estudo da Função Quadrática, é muito parecido com os conceitos e aplicações da Função Afim, entretanto o comportamento da Função Quadrática e diferente da Função Afim, é justamente isso que vamos estudar:
O gráfico da função quadrática corresponde a uma curva muito especial em Matemática chamada parábola. A parábola é uma curva do plano cujos pontos satisfazem uma condição bem definida.
Assistam os vídeos, vejam as aplicações bem como a forma geral de representar uma função quadrática, e faça um estudo comparativo utilizando a Apostila 2:
Um Forte Abraço
Prof Renata S
Função Linear: Coeficiente Angular; Coeficiente Linear; Crescente e Decrescente - 1º ano - Ensino Médio
Olá Queridos Alunos:
Vamos falar um pouco da Função Afim:
Nos estudamos uma Função Afim, através das funções horárias da física. Entretanto esse assunto requer um atenção maior, pois precisamos analisar os conceitos da Função Afim assim o conceito entendido você não esquecerá mais!
Definição da Função Afim:
Um casal resolve realizar uma viagem ao Rio de Janeiro. Para isso,separa os valores referentes ao combustível e o pedágio, o que representa R$ 75,00. A hospedage, com diária completa (café da manhã, almoço e jantar), sai por R$ 130,00 o casal. Quanto custará essa viagem?
Nessa situação,temos um gasto fixo correspondente ao combustível e ao padágio, que independe da quantidade de dias que o casal ficará hospedado. E temos um valor variável,correspondente ao número de diárias. Assim,o gasto do casal será composto destas duas parcelas.
Valor Gasto = (valor do combustível + valor do pedágio) + valor total das diárias.
Logo, se o casal ficar hospedado durante dois dias pagará: Valor Gasto = 75,00 + 130x2 (2 dias da hospedagem), então o valor a ser pago será: 75 + 130*2 = 75 + 230 = 335.
Percebemos que o valor gasto - g(x) na viagem é função da quantidade x de dias de hospedagem. Assim: g(x) = 75 + 130*x
Essa sentença é um exemplo de lei de formação de uma função afim.
Definição: f:IR->IR chama-se função afim quando existem números reais a e b tal que f(x) = ax + b, para todo x Real.
Assistam os vídeos, e comparem com as explicações da Apostila, assim ficará mais fácil resolver os exercícios.
Um Forte Abraço.
Profª Renata S
Vamos falar um pouco da Função Afim:
Nos estudamos uma Função Afim, através das funções horárias da física. Entretanto esse assunto requer um atenção maior, pois precisamos analisar os conceitos da Função Afim assim o conceito entendido você não esquecerá mais!
Definição da Função Afim:
Um casal resolve realizar uma viagem ao Rio de Janeiro. Para isso,separa os valores referentes ao combustível e o pedágio, o que representa R$ 75,00. A hospedage, com diária completa (café da manhã, almoço e jantar), sai por R$ 130,00 o casal. Quanto custará essa viagem?
Nessa situação,temos um gasto fixo correspondente ao combustível e ao padágio, que independe da quantidade de dias que o casal ficará hospedado. E temos um valor variável,correspondente ao número de diárias. Assim,o gasto do casal será composto destas duas parcelas.
Valor Gasto = (valor do combustível + valor do pedágio) + valor total das diárias.
Logo, se o casal ficar hospedado durante dois dias pagará: Valor Gasto = 75,00 + 130x2 (2 dias da hospedagem), então o valor a ser pago será: 75 + 130*2 = 75 + 230 = 335.
Percebemos que o valor gasto - g(x) na viagem é função da quantidade x de dias de hospedagem. Assim: g(x) = 75 + 130*x
Essa sentença é um exemplo de lei de formação de uma função afim.
Definição: f:IR->IR chama-se função afim quando existem números reais a e b tal que f(x) = ax + b, para todo x Real.
Assistam os vídeos, e comparem com as explicações da Apostila, assim ficará mais fácil resolver os exercícios.
Um Forte Abraço.
Profª Renata S
1 de abril de 2012
Volume: Pirâmide; Cone e Esfera - 2º Ano do Ensino Médio.
Olá Queridos Alunos
Assistam com muito atenção os vídeos abaixo, façam as devidas anotações, e estudem o conteúdo da "Apostila". É de extrema importância assistir mais de uma vez aos vídeos.
Parte I:
Parte II:
Não esqueçam: DEDICAÇÃO TOTAL AOS ESTUDOS! ESSA É A ÚNICA SAÍDA PARA O SUCESSO ESCOLAR...
Deixe suas dúvidas ou comentário sobre os vídeos, ou dos exercícios da apostila.
Um Forte Abraço.
Prof Renata S
Assistam com muito atenção os vídeos abaixo, façam as devidas anotações, e estudem o conteúdo da "Apostila". É de extrema importância assistir mais de uma vez aos vídeos.
Parte I:
Parte II:
Não esqueçam: DEDICAÇÃO TOTAL AOS ESTUDOS! ESSA É A ÚNICA SAÍDA PARA O SUCESSO ESCOLAR...
Deixe suas dúvidas ou comentário sobre os vídeos, ou dos exercícios da apostila.
Um Forte Abraço.
Prof Renata S
Estudo do Sinal de uma Função e Tipos de Função: Sobrejetora; Injetora e Bijetora; Composta e Inversa: 1º Ano: Ensino Médio.
Olá Queridos Alunos:
Quando estudamos funções, fazemos o estudo do "Sinal", na realidade o estudo do sinal de uma função tem como parâmetro o conjunto "Imagem" (eixo das ordenadas "y"), logo a nossa pergunta tem que ser: Para que valores Reais o "Domínio" (eixo das abscissas "x") tem uma Imagem, maior que zero ou menor que zero... Logo, precisamos fazer o estudo do sinal para responder para que valores do domínio temos uma imagem positiva ou negativa.
Agora, quando o assunto é função, podemos classificar-las, de acordo com a sua IMAGEM-CONTRA DOMÍNIO: Tipos de Funções: Sobrejetora; Injetora e Bijetora... Leiam as páginas da Aposital 25 a 27, e assistam o vídeo para ter a real compreensão do assunto.
FUNÇÃO COMPOSTO:
Função Composta, é quando o Domínio de uma Função é uma outra Função! Como assim: Temos uma função f: sendo o seu domínio a função g: Isso quer dizer que no lugar do domínio vamos colocar a função g: f(g(x)) ou (fºg)(x). Exemplo: Se f(x) = 2x - 1, e g(x) = -3x + 5, como a função g(x) e o domínio da função f(x), temos: f(g(x))= 2.g(x) -1; onde f(g(x)) = 2(-3x + 5) -1, essa é a função composta de f(g(x)). Leiam as páginas 26 a 27 da apostila e assistam o video abaixo:
FUNÇÃO INVERSA:
Função Inversa é quando o Y quer perguntar! Como assim? Quando o Y (imagem) quer pegar o lugar do Domínio X, quer dizer: Inverte-se os papéis: o y pergunta e o x responde, então na função f: substituimos as variáveis x e y: no lugar do x colocamos o y e no lugar do y colocamos o x... Assistam o vídeo, leiam com atenção as páginas 27 a 29 da apostila.
Após Estudar as páginas e assistir os vídeos, deixe o seu comentário sobre o que você entendeu ou a sua dúvida sobre os conteúdos expostos.
Um Forte Abraço.
Prof Renata S
Quando estudamos funções, fazemos o estudo do "Sinal", na realidade o estudo do sinal de uma função tem como parâmetro o conjunto "Imagem" (eixo das ordenadas "y"), logo a nossa pergunta tem que ser: Para que valores Reais o "Domínio" (eixo das abscissas "x") tem uma Imagem, maior que zero ou menor que zero... Logo, precisamos fazer o estudo do sinal para responder para que valores do domínio temos uma imagem positiva ou negativa.
Agora, quando o assunto é função, podemos classificar-las, de acordo com a sua IMAGEM-CONTRA DOMÍNIO: Tipos de Funções: Sobrejetora; Injetora e Bijetora... Leiam as páginas da Aposital 25 a 27, e assistam o vídeo para ter a real compreensão do assunto.
FUNÇÃO COMPOSTO:
Função Composta, é quando o Domínio de uma Função é uma outra Função! Como assim: Temos uma função f: sendo o seu domínio a função g: Isso quer dizer que no lugar do domínio vamos colocar a função g: f(g(x)) ou (fºg)(x). Exemplo: Se f(x) = 2x - 1, e g(x) = -3x + 5, como a função g(x) e o domínio da função f(x), temos: f(g(x))= 2.g(x) -1; onde f(g(x)) = 2(-3x + 5) -1, essa é a função composta de f(g(x)). Leiam as páginas 26 a 27 da apostila e assistam o video abaixo:
FUNÇÃO INVERSA:
Função Inversa é quando o Y quer perguntar! Como assim? Quando o Y (imagem) quer pegar o lugar do Domínio X, quer dizer: Inverte-se os papéis: o y pergunta e o x responde, então na função f: substituimos as variáveis x e y: no lugar do x colocamos o y e no lugar do y colocamos o x... Assistam o vídeo, leiam com atenção as páginas 27 a 29 da apostila.
Após Estudar as páginas e assistir os vídeos, deixe o seu comentário sobre o que você entendeu ou a sua dúvida sobre os conteúdos expostos.
Um Forte Abraço.
Prof Renata S
Assinar:
Comentários (Atom)


