
O que é o espaço?
Reconhecemos e usamos o espaço, mas se alguém perguntar o que é o espaço, muitos irão ter dificuldades em explicar. Na verdade, é mais fácil explicar o que se pode fazer com este ente primitivo que não tem definição para nós.
Uma primeira tentativa para explicar isto, é dizer que é tudo o que nos envolve e é o local onde podemos nos mover para a frente, para o lado e para cima.
Pelo conceito expresso, observamos que vivemos em um ambiente tridimensional. Basta então conhecer as três direções para identificar a posição relativa que ocupamos.
Quando afirmamos que vamos andar para a frente, para o lado e para cima, devemos quantificar e identificar o quanto iremos nos deslocar nestas direções, logo necessitamos conhecer uma origem para o sistema e identificar este ponto como
(0,0,0) pois esperamos que ele esteja localizado a uma distância num ponto de referência para todos os outros pontos.
O Sistema Cartesiano tridimensional
Um procedimento matemático simples é tomar um ponto genérico como:
P=(x,y,z)
onde x indicará a quantidade deslocada na direção positiva do eixo que contem os deslocamentos para frente, y indicará a quantidade deslocada na direção positiva do eixo que contem os deslocamentos para o lado e z indicará a quantidade deslocada na direção positiva do eixo que contem os deslocamentos para cima.
Para facilitar as coisas do ponto de vista matemático, iremos denominar tais direções por: Eixo OX, Eixo OY e Eixo OZ.
O sistema tridimensional é o conjunto de todos os ternos ordenados (x,y,z), sendo que ordem não pode ser mudada sob pena de nos deslocarmos para outro lugar. A palavra cartesiano se deve a René Descartes, conhecido como cartesius. x recebe o nome de abscissa, y o nome de afastamento e z o nome de cota.
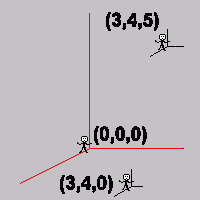
Exemplo: Se um indivíduo está no centro da cidade em uma posição O(0,0,0) e quer andar para a frente 3 quadras, depois andar para o lado 5 quadras e depois subir até o 10º andar de um prédio a posição final do mesmo após o percurso será o ponto P(3,5,10), e podemos observar que as unidades não são necessariamente as mesmas. Se este mesmo indivíduo se deslocasse para a posição final P(3,10,5), certamente chegaria a um lugar diferente.
Podemos,observar que em atividades simples do nosso dia-a-dia, existe a aplicação da conceitos que aprendemos na sala de aula, pois a matemática está em todos os lugares.
Por exemplo: Qual o conceito de corpo, na geometria? Resposta: Corpo é tudo quanto ocupa lugar no espaço.
Agora, é com você!Faça um breve comentário do conteúdo postado. Será que existem outras aplicações relacionadas, a contribuição feita para matemática, de René Descartes?
Fonte de pesquisa:
http://pessoal.sercomtel.com.br/matematica/geometria/espaco/espaco.htm
Prof. Eu estava fazendo uns exercicíos que encontrei na internet e me deparei com um que me deixou com muuuuita duvida! Não consegui copiar pq dá erro mas consegui o link: http://www.cocimperatriz.com.br/2007/doc/listaoexercicios/1listaomatmarlon2ano.pdf
ResponderExcluirÉ o exercício 11 do Mackenzie. Dá uma olhada por favor pq eu achei que ele fosse parecido com o exercício 3 da página 12.
Olá Mariana
ExcluirNa próxima quinta-feira eu levo o exercício para fazermos na sala de aula. Teremos uma atividade valendo, por favor avisa o pessoal.
Abraços
Prof Renata
Profº Achei super interessante o conteúdo, porem o conceito é bem mais simples do que o desenvolvimento dos exercícios, procurei na internet alguns exercícios prontos, ficou mais claro para entender. Porem ainda tenho um pouco de duvida para interpretar o que se pede.
ResponderExcluirCamila Moura 3º ano ensino médio. (CADI)
Olá Camila
ResponderExcluirGostei dos exercícios da lista do site da Mariana. Acho que vou utilizar-los na atividade... Isso mesmo Camila, estudar exercícios já resolvidos ou assistir vídeos aulas, é um recurso excelente. No caso da interpretação: Separe as informações dadas pelo exercício; o que ele pede; e depois análise estratégia de cálculo para responder a pergunta.
Abraços
Prof Renata
Abraços
Prof Renata
Oi profª o conceito eu entendi, mas na resolução dos problemas estou tendo bastante dificuldade :/ (CADI)
ResponderExcluirOlá Ana
ExcluirNa verdade sua dificuldade está na interpretação e na execução dos mesmos. E, preciso anotar os pontos importanto e descrever qual o processo de cálculo para cada situação.
Abraços
Prof Renata
É Professora, tambem nao estou conseguindo resolver os exercicios. Procurei alguns resolvidos, mas estão muito mal explicados. (CADI)
ResponderExcluirOlá Caique
ResponderExcluirEntão, marque a sua dúvida do lado de cada exercicio, para que amanhã possamos corrigir juntos e assim supri todas as dúvidas.
Abraços
Prof Renata
Oi Profº, eu peguei alguns exercícios da apostila da Poli para resolver, estou muito feliz por ter conseguido fazê-los, acho que finalmente estou entendendo a matéria, já o conceito de espaço eu não entendi muito bem o eixo de Z.
ResponderExcluirAbraçõs (CADI)
Olá Ana
ExcluirÉ isso ai, assim com certeza vc vai entender tudo! Agora a ideia de espaço é justamente essa, quando estamos estudando figuras geométricas estamos analisando dentro de dois eixos x e y (plano), entretanto quando estamos em três dimensões é porque estamos em um espaço tridimensiona formado por três eixos (x, y e z).
Abraços
Prof Renata
Profª Bom dia !
ResponderExcluirEntão pro, eu estava refazendo alguns exercicios da apostila, e na pagina 7 exe.4 ( MACKENZIE)eu resolvi de maneira diferente da correção, mas deu o mesmo resultado... gostaria de saber se tem algo errado.
Minha resoluçao ficou assim:
1º Encontrei o ponto medio de AB depois de BC que deu AB=(2,2/k)e AC=(5/2,1/2)
2ºMontei a matriz que deu: (2+5/k+3)-(5/2+1+k)=> 5k/4+3-5/2-1-k=2/10 (0,20)
=> ( quem estava dividindo passou a multiplicar) 4(5k+3)-2(5-1-k)=2/10 => 20k+12-10-2-2k=2/10 =>20k-2k=2/10 =18 x 2/10 ( simplificando => 1/5) = 18/5
É isso Profª...
Abraços, Sthefanie N. (CADI)
Olá Sthefanie
ExcluirO ponto médio de AB é (2, k/2);O ponto médio qe vc chamou de AC na verdade é o BC (5/2, 1/2). A área do triângulo que é igual a 0,20 foi formada pelos pontos: AB, BC e C, com essas coordenadas vc monta a matriz e diz que o determinante é igual a zero. Agora, equação: 20k - 2k = 2/10 fica assim: 18k = 2/10 sendo: k = (2/10): 18, divisão de frações: k = (2/10)x(1/18),o inverso de 18: Logo o valor de k é 2/180, simplificando fica k = 1/90... Não podemos esquecer que estamos dentro do módulo então consideramos dois valores reais.
Abraços
Prof Renata
Sthefanie
ResponderExcluirParabéns por estar estudando e participando do Blog: Esse é um espaço criado para vocês.
Abraços
Obrigada Profª, nao estou fazendo mais que minha obrigação como diz minha mãe kkk... Esse blog me ajuda bastante, pois tenho dificuldades em mat. e tenho muita vergonha de perguntar em classe tambem, aqui felizmente nao tenho isso...
Excluirquando resolvi esse exercicio o ponto medio AC esta BC em minha folha, foi na hora de digitar que me confundi ... desculpa. Tenho somente uma duvida pro, o exercico nos da 5 alternativas a)6/5 b)12/5 c)18/5 d)4 e e)5 a resposta neste caso, seria 18/5 mesmo?
Olá Sthefanie
ExcluirMais na sala vc pode me chamar, e falar a sua dúvida. A resposta certa é a letra c (18/5). Mais do que a obrigação, a busca do conhecimento nos faz evoluir tanto como pessoa, bem como nação. Aprender é bom, e é claro, como tudo precisamos dedicar um pouco do nosso tempo para isso.
Abraços
Prof Renata
Olá prô, estava revisando uns exercícios da apostila, e estou com dúvida na resolução do exercício 6 da pág 13. Seria possível revisá-lo na sala ?
ResponderExcluirUm beijo e um abraço. Lindsay
Olá Lindsay
ResponderExcluirSim, mais conforme diz o enunciado se o triângulo está sendo formado com pelos eixos, isso quer dizer: quando x for igual a 0, substituimos no lugar do x o 0 e achamos o y. Agora, quando o y for igual a 0, substituimos no o y por 0 e achamos o x, logo achamos dois pontos, o terceiro ponto é o ponto de origem, com os três pontos montamos a matriz, e assim achamos o valor de m.
Abraços
Prof Renata