
O que é o espaço?
Reconhecemos e usamos o espaço, mas se alguém perguntar o que é o espaço, muitos irão ter dificuldades em explicar. Na verdade, é mais fácil explicar o que se pode fazer com este ente primitivo que não tem definição para nós.
Uma primeira tentativa para explicar isto, é dizer que é tudo o que nos envolve e é o local onde podemos nos mover para a frente, para o lado e para cima.
Pelo conceito expresso, observamos que vivemos em um ambiente tridimensional. Basta então conhecer as três direções para identificar a posição relativa que ocupamos.
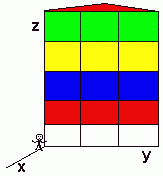
Quando afirmamos que vamos andar para a frente, para o lado e para cima, devemos quantificar e identificar o quanto iremos nos deslocar nestas direções, logo necessitamos conhecer uma origem para o sistema e identificar este ponto como
(0,0,0) pois esperamos que ele esteja localizado a uma distância num ponto de referência para todos os outros pontos.
O Sistema Cartesiano tridimensional
Um procedimento matemático simples é tomar um ponto genérico como:
P=(x,y,z)
onde x indicará a quantidade deslocada na direção positiva do eixo que contem os deslocamentos para frente, y indicará a quantidade deslocada na direção positiva do eixo que contem os deslocamentos para o lado e z indicará a quantidade deslocada na direção positiva do eixo que contem os deslocamentos para cima.
Para facilitar as coisas do ponto de vista matemático, iremos denominar tais direções por: Eixo OX, Eixo OY e Eixo OZ.
O sistema tridimensional é o conjunto de todos os ternos ordenados (x,y,z), sendo que ordem não pode ser mudada sob pena de nos deslocarmos para outro lugar. A palavra cartesiano se deve a René Descartes, conhecido como cartesius. x recebe o nome de abscissa, y o nome de afastamento e z o nome de cota.
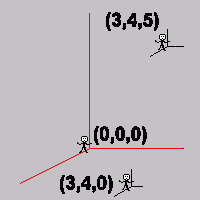
Exemplo: Se um indivíduo está no centro da cidade em uma posição O(0,0,0) e quer andar para a frente 3 quadras, depois andar para o lado 5 quadras e depois subir até o 10º andar de um prédio a posição final do mesmo após o percurso será o ponto P(3,5,10), e podemos observar que as unidades não são necessariamente as mesmas. Se este mesmo indivíduo se deslocasse para a posição final P(3,10,5), certamente chegaria a um lugar diferente.
Podemos,observar que em atividades simples do nosso dia-a-dia, existe a aplicação da conceitos que aprendemos na sala de aula, pois a matemática está em todos os lugares.
Por exemplo: Qual o conceito de corpo, na geometria? Resposta:
Corpo é tudo quanto ocupa lugar no espaço.
Agora, é com você!
Faça um breve comentário do conteúdo postado. Será que existem outras aplicações relacionadas, a contribuição feita para matemática, de René Descartes?
Fonte de pesquisa:
http://pessoal.sercomtel.com.br/matematica/geometria/espaco/espaco.htm





