EE LEDA: 3ºANOS A, B e C - FÍSICA: TRABALHO 2 e TRABALHO 3 - REVISÃO: FÍSICA DO M

 Olá Queridos Alunos 

Estamos Finalizando as Atividades do 4ºBimestre: 

https://www.youtube.com/watch?v=6Ed3U6kBg9g&list=PLECgu9L1iHiEP9B1blf6pAbqm4iGHcYal&index=2

Aula 2 - A Dinâmica do Movimento. 

LINK DO TRABALHO 2 -  ACESSAR:

TRABALHO 2 - Movimento Dinâmico

https://www.youtube.com/watch?v=lRxLzYJIV2A&list=PLECgu9L1iHiEP9B1blf6pAbqm4iGHcYal&index=3

Aula 3: Energia em Transformação. 

LINK DO TRABALHO 3 - ACESSAR:

TRABALHO 3 - ENERGIA EM TRANSFORMAÇÃO

TODOS PRECISAM  FAZER! MESMO QUEM ESTÁ DEVENDO ATIVIDADES DE OUTROS BIMESTRES... 

DISPONÍVEL ATÉ O DIA 08/12/2020. 

Um Forte Abraço 

Profª Renata Spinelli 

 

EE LEDA: 2ºA, B e C - TRABALHO DE FÍSICA: ESPELHOS - PLANOS, CÔNCAVOS, CONVEXOS e FORMAÇÃO DE IMAGEM.

 Olá Queridos Alunos 

Segue o último "Trabalho" para compor a Nota desde ano... Parabéns para todos que ficaram firmes durante o ano inteiro, sabemos que não foi fácil pra ninguém... Aqueles, que estão devendo atividades, aproveitem para fazer!... 

Assistam a vídeo aula abaixo:

                                            Telecurso 2000 - aula 32: Espelhos 

 

Assistiu? Agora, preencha o Link da Atividade Avaliativa... 

Acessar. 

LISTA DE CHAMADA e ATIVIDADE AVALIATIVA

Um Forte Abraço

E.E. LEDA - 2ºANO A, B e C: REFLEXÃO E REFRAÇÃO DA LUZ - TELECURSO 2000 AULAS 31 e 33 (AULA 23/11/2020)

 Olá Queridos Alunos 

Nossa Jornada está chegando ao "Fim"... Para Encerrar o 4ºBimestre, serão disponíveis duas Atividades: 

Primeira Semana: 23/11/2020 à 30/11/2020 - Leis da Reflexão e Refração da Luz  

Segunda Semana: 01/12/2020 à 07/12/2020 - Espelhos  

No dia 07/12, teremos uma aula no Googlemeet de Encerramento. 

                                 Telecurso 2000, aula 31: Fenômeno de "Reflexão". 

https://www.youtube.com/watch?v=k0gFrUlWJuQ&list=PL2EDB3FBFFCBAE769&index=31

ATENÇÃO LINK DA AULA 31: LEIS DA REFLEXÃO E REFRAÇÃO DA LUZ. 

Acessar o Link da Aula 1.... 

https://forms.gle/Qo7MR9G15MWqJs6F9

Telecurso 2000, aula 33: Fenômeno da "Refração". 

https://www.youtube.com/watch?v=Q6lOHU0gWO0&list=PL2EDB3FBFFCBAE769&index=33

Acessar o Link da aula de Refração - AGORA DISPONÍVEL

https://forms.gle/tP6kW1xV2vm7tQhN9

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA: 3º ANO A, B e C - DISCIPLINA DE FÍSICA - TRABALHO 1: "MOVIMENTOS".

 Olá Queridos Alunos 

Nossa jornada está chegando ao final, para finalizar o 4ºBimestre, teremos TRÊS trabalhos, o primeiro está DISPONÍVEL "hoje"... Vocês irão assistir a vídeo do CEEJA - Mundo do Trabalho, e preencher o LINK, COM O QUESTIONÁRIO AVALIATIVO... 

                                          VÍDEO TEMA: MOVIMENTO 

Acessar e Responder o Link do TRABALHO: 

TRABALHO DE FÍSICA - MOVIMENTO PARTE 1

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA - 2ºANO A, B e C - Aula dia 09/11/2020 - Aula de Física: Correção de Exercícios - Propagação da Luz.

 Olá Queridos Alunos 

Segue a Lista de Chamada da última aula... ASSISTAM A AULA, E DEPOIS NÃO DEIXEM DE PREENCHER A LISTA DE CHAMADA. 

Aula: 09/11/2020

LISTA DE CHMADA: 09/11/2020 - LINK 

LISTA DE CHAMADA - 09/11/2020

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA: 9ºANO A, B e C - AULAS DOS DIAS: 22/10/2020 e 23/10/2020: "SEMELHANÇA DE FIGURAS PROPORCIONAIS" - Lados Correspondentes; Ângulos Congruentes e Fator de Semelhança.

 Olá Queridos Alunos 

Atenção Turmaa.... Assistam as aulas, anotem as correções, e comentários mencionadas na aula... 

FAZER TAMBÉM DO LIVRO DIDÁTICO:

PÁGINAS 163, 166, 167 e 169... 

Não esqueçam da Apostila "Aprender Sempre", para nossa próxima aula:

Aula dia 23/10/2020 - Assistir. 

Aula dia 22/10/2020 - Assistir. 

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA - 3ºANO A, B e C - AULA DO DIA 27/11/2020: ENEM/2021 - ONDAS LUMINOSAS - CORREÇÃO COMENTADA DOS EXERCÍCIOS...

 Olá Queridos Alunos 

Segue a aula do dia 27/10/2020, com a Lista de CHAMADA DA AULA:

Assistir a aula:

    LINK DA LISTA DE CHAMADA, ACESSAR:

LISTA DE CHAMADA - AULA: 27 DE OUTUBRO DE 2020

DISPONÍVEL ATÉ A PRÓXIMA QUARTA-FEIRA 04/11/2020. 

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA: 2ºANO A, B e C - AULA DE FÍSICA DIA 26/10/2020. CORREÇÃO DE EXERCÍCIOS - PROPAGAÇÃO RETILÍNEA DA LUZ.

 Olá Queridos Alunos 

Segue a aula do dia 26/10/2020, com a "Lista de Chamada"... 

Aula - Assistir... 

LINK DA LISTA DE CHAMADA:

LISTA DE CHAMADA AULA DIA 26 DE OUTUBRO DE 2020

Disponível até ATÉ 04/11/2020... 

Um Forte Abraço 

Profª Renata Spinelli 

E.E LEDA - 3º ANO A, B e C: AULA DE FÍSICA - 20/10/2020: REVISÃO ENEM/2021 - LISTA DE CHAMADA COM ATIVIDADE: CONTEÚDO: COMPORTAMENTO RETILÍNEO DA LUZ.

 Olá Queridos Alunos 

Assistam Aula de Hoje!!! Não esqueçam de anotarem os exercícios resolvidos no caderno... 

Acessar o "LINK" abaixo!!!! 

LISTA DE CHAMADA - 20/10/2020 COM ATIVIDADE.

Um Forte Abraço

Profª Renata Spinelli 

E.E. LEDA: 2ANO A, B e C - AULA DE FÍSICA DATA: 19/10/2020 - CORREÇÃO EXERCÍCIO PÁG. 130 - EX 4... PROPAGAÇÃO RETILÍNEA DA LUZ

 Olá Queridos Alunos 

Assistam a aula do dia 19/10/2020, façam as anotações e correções dos "Exercícios" corrigidos durante a aula...EXERCÍCIOS DE ATIVIDADE: PÁGINA 131 - FAZER PARA ENVIAR NO LINK DA CHAMADA: EP6, EP7, EP8, EP10 e EP11... FAÇAM OS PROCESSOS, EM CASO DÚVIDAS... NA RESOLUÇÃO COLOQUEM "FIQUEI COM DÚVIDA NESSE EXERCÍCIO"... ATENÇÃO: NÃO VOU ACEITAR COPIA DA INTERNET!!!1 

Aula: 19/10/2020

    LINK DA LISTA DE CHAMADA E DA ATIVIDADE - ENVIAR ATÉ DOMINGO... 

LISTA DE CHAMADA COM ATIVIDADE - AULA: 19/10/2020

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA: 3º ANO A, B e C: FÍSICA - AULA: 06/10/2020 - REVISÃO ENEM/2020 - CONTEÚDO: ESTUDO DA LUZ - FOTÓNS E PROPAGAÇÃO DA LUZ.

 Olá Queridos Alunos 

Estamos fazendo uma revisão para o ENEM/2020... Sua participação é extrema importância, para essa revisão... Na discutimos conceitos da Propagação da Luz... 

Assistam a aula do dia 06/10/2020,  responda a "LISTA DE CHAMADA"... NO LINK ABAIXO DA AULA. 

AULA DIA 06/10/2020

ACESSAR O LINK ABAIXO DA CHAMADA

LISTA DA CHAMADA AULA 06/10/2020 - COM ATIVIDADE

Um Forte Abraço

Profª Renata Spinelli 

EE LEDA: 2º ANO A, B e C - FÍSICA - AULA DIA 05/10/2020: Conteúdo - PROPAGAÇÃO DA LUZ. Resolução de Exercícios

 Olá Queridos Alunos 

Na última aula, discutidos e resolvemos exercícios que envolvem a "PROPAGAÇÃO DA LUZ" no meio... 

Assistam a aula, e respondam a Lista de Chamada!!!  

LISTA DE CHAMADA 05/10/2020, COM ATIVIDADE

LIÇÃO DE CASA: NÃO ESQUEÇAM DE FAZER OS EXERCÍCIOS DO NOSSO LIVRO DE FÍSICA PÁGINA 131. 

Um Forte Abraço 

Profª Renata Spinelli 

EE Profª Leda - 9º ano A, B e C - Aulas dos dias 01/10/2020 e 02/10/2020 - Correção Comentada Equação do Segundo - Problemas com Áreas

 Olá Queridos Alunos 

Estou enviando as aulas dos dias 01/10/2020 e 02/10/2020, com o conteúdo envolvendo o Teorema de Pitágoras, Bháskara - problemas de área. 

Aula 1: 

Aula 2:

Como Atividade vocês terão que enviar as correções feitas nas aulas dos dias 01/10 e 02/10, que estão no caderno... Também, os exercícios da página 103 - Exercícios 16, 17, 18, 19, 20  e 21. Tirar Foto e Enviar até quinta-feira 08/10/2020, para o E-mail: renataspinelli.leda@gmail.com

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA: 3º ANO A, B e C - ATIVIDADE DE FÍSICA (CMSP): HISTÓRIA E ORIGEM DO FOTÓN... DISCIPLINA DE FÍSICA. ENEM/2020.

 Olá Queridos Alunos 

HOJE, VAMOS VIAJAR PARA O SÉCULO XX - ONDE A FÍSICA QUÂNTICA SURGIU... VER SOCIEDADE, CARROS E TELEFONE DO SEC XIX... E, COMPARA COM O SÉC XXI... REALMENTE É DEMAIS.... 

AGORA, É COM VOCÊS! ASSISTAM AO VÍDEO DISPONÍVEL

PRESTEM ATENÇÃO NAS DISCUSSÕES QUE EXISTIAM ENTRE OS FÍSICOS DA ÉPOCA, E CONCLUSÃO FINAL... VOCÊS TERÃO ATÉ QUINTA-FEIRA 01/10/2020, PARA REALIZAR A ATIVIDADE DO LINK ABAIXO: 

LISTA DE CHAMADA AULA 29/09/2020 - HISTÓRIA DA ORIGEM DO FÓTONS

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA: 2ºANO A. B e C - AULA DE FÍSICA - 28/09/2020. CONCEITOS BÁSICOS DE ÓPTICA.

 Olá Queridos Alunos 

Hoje, estudamos os conceitos Básicos da Óptica: Feixes, Propagação da Luz; Superfície.... Sombra e Penumbra.

 

Aula do dia: 28/09/2020

NÃO ESQUEÇA DE GARANTIR SUA PARTICIPAÇÃO E NOTA, APÓS ASSISTIR A AULA DO DIA 28/09/2020. 

ACESSAR O LINK, ABAIXO:

LISTA DE CHAMADA DO DIA 28/09/2020

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA: 9ºANO A, B e C - Aula de Matemática dia 25/09/2020 "MMR - TEOREMA DE PITÁGORAS - NOMEANDO OS NÚMEROS REAIS.

 Olá Queridos Alunos 

Aprender Sempre" deve ser Nosso Objetivo Sempre!!! Nessa aula estudamos o Teorema de Pitágoras - envolvendo outros conceitos: Conjunto dos Números Reais; Equação do Segundo Grau.... 

Você poderá assistir novamente a aula.... Assim, sua aprendizagem será completa:

Antes de acessar o Link abaixo: "PESQUISA A HISTÓRIA DE PITÁGORAS, E SUA IMPORTÂNCIA PARA OS DIAS DE HOJE"... APÓS, FAZER ESSA PESQUISA, ACESSAR O LINK E RESPONDER...

LISTA DE CHAMADA DO DIA 25/09/2020 - HISTÓRIA DE PITÁGORAS. 

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA - 2ºANO A, B e C: (LISTA DE CHAMADA-DATA: 21/09/2020) AULA DE FÍSICA - CORREÇÃO COMENTADOS DE EXERCÍCIOS.... CONCEITOS E APLICAÇÕES.

 Olá Queridos Alunos

Segue a Lista de Chamada da aula do dia 21/09/2020...Assim, que aula estiver disponível, vou por aqui no BLOG.... 

ACESSAR O LINK, ABAIXO:

LISTA DE CHAMADA AULA: 21/09/2020. 

Um Forte Abraço 

Profª Renata Spinelli

EE LEDA - 3ºA, B e C - AULA DE FÍSICA (LISTA DE CHAMADA) : 15/09/2020 e 22/09/2020 - ENEM/2020: REVISÃO ONDAS MECÂNICAS E LUMINOSAS....

 Olá Querido Aluno

Segue as aulas dos duas 15/09 e 22/09... Antes de responder a Lista de Chamada, ASSISTAM A AULA, ANOTEM OS EXERCÍCIOS CORRIGIDOS!!!! 

AULA 1:

AULA 2:

LISTA DE CHAMADA, COM OS EXERCÍCIOS PARA ENVIAR ESTÃO DISPONÍVEL NO LINK, ABAIXO:

LISTA DE CHAMADA: 15/09/2020 e 22/09/2020 - EXERCÍCIOS E PRESENÇA

DISPONÍVEL ATÉ SEGUNDA-FEIRA 29/09/2020

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA: 9º ANO A, B e C (MATEMÁTICA) - AULA 17/09/2020 - SITUAÇÕES ENVOLVENDO EQUAÇÕES DO SEGUNDO GRAU - BHASKARA.

 Olá Queridos Alunos

Resolver Situações Envolvendo Equações do Segundo Grau, envolve intepretação e estratégia de cálculo, não podemos esquecer do "MÉTODO DE POLYA" as estratégias para um resolver diversos tipos de problemas... 

Assistam aula, não esqueçam de anotar, o exercícios resolvidos não... Lembre-se, "Você" precisa enviar os exercícios por e-mail, para garantir sua participação na aula.. E-mail: renataspinelli.leda@gmail.com

Um Forte Abraço

Profª Renata Spinelli 

EE LEDA - Aula dia 14/09/2020: FÍSICA - CORREÇÃO EXERCÍCIOS DO LIVRO DE FÍSICA.

 Olá Queridos Alunos 

Segue a aula de Hoje, com a Lista de Chamada: 

Conteúdo: Pertubação de uma onda sonoro - equação geral da propagação de uma Onda Sonora ou Luminosa... 

Assistir a aula do dia 14/09/2020

Acessar o Link da Lista de Chamada e Exercícios... 

LISTA DE CHAMADA AULA DIA 14/09/2020: COM EXERCÍCIOS DE APRENDIZAGEM

Um Forte Abraço 

Profª Renata Spinelli 

Aulas 10/09/2020 e 11/09/2020 do 9º ANO A, B e C- MATEMÁTICA - MMR: ESTUDO DOS NÚMEROS RACIONAIS "CONTINUAÇÃO"; SISTEMAS DE EQUAÇÕES DO 1ºGRAU E EQUAÇÃO DO 2º GRAU.

 Olá Queridos Alunos 

Conteúdo Estudado: MMR - "Retomada" Operações com os Números Racionais: MMC, MDC, Soma, Subtração, Multiplicação, Divisão de Fração. Revisamos: Fração Própria, Imprópria e Número Misto - Sistemas de Equações com uma Incógnita - Área, Perímetro. 

Continuação do Conteúdo do 9º ano: Situações Problemas (Interpretações) envolvendo a Fórmula de 

Bhaskara... 

                                            Assista a aula 10/09/2020. 

Assista a aula 11/09/2020

Após Assistir as Aulas - Assine a Lista de Chamada no Link Abaixo... 

LISTA DE CHAMADA 10/09 e 11/09... MATEMÁTICA

ATENÇÃO: AGUARDE UMA NOVA LISTA DE EXERCÍCIO...

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA: 9 anos A, B e C - Matemática: Revisão "MMR" - Operações com os RACIONAIS; MÚLTIPLOS; DIVISORES E EQUAÇÃO DO SEGUNDO GRAU. Data das Aulas:03/09/2020 e 04/09/2020.

 Olá Queridos Alunos

Precisamos estar "APRENDENDO SEMPRE"... POR ASSISTAM AS AULAS QUE ESTÃO DISPONÍVEL, ANOTEM OS EXERCÍCIOS CORRIGIDOS E COMENTADOS NO CADERNO. 

                                            Aula 1:

                                             Aula 2. 

ACESSAR O LINK ABAIXO - PARA NOTA DE PARTICIPAÇÃO E PRESENÇA. 

LISTA DE CHAMADA - 9º ANO A, B e C - AULAS DOS DIAS 03/09 E 04/09

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA - 9º ANOS A, B e C: MATEMÁTICA - PERÍODO DAS AULAS: 17/08/2020 À 21/08/2020 "CMSP" RADICIAÇÃO; FATORAÇÃO; PRODUTO NOTÁVEL E EQUAÇÃO DO SEGUNDO.

 Queridos Alunos 

Vamos Retomar os Conteúdos Estudados nessa semana!!! Assistam as aulas, anotem os exercícios discutidos e corrigidos durante as aulas... Importante, estar "SEMPRE APRENDENDO"... 

                                            Aula 1:

Aula 2:                                                                  

Aula 3:                                                              

Aula 4:                                                              

Um Forte Abraço 

Profª Renata Spinelli

E.E. LEDA - LISTA DE CHAMADA 08/09/2020 - AULA DE FÍSICA: 3º ANOS A, B e C - REVISÃO ENEM: NATUREZA DA ONDA

 Olá Queridos Alunos 

ASSISTA A NOSSA AULA

APÓS ASSISTIREM A AULA - ACESSAR O LINK E RESPONDER: O LINK - FICARÁ DISPONÍVEL ATÉ SEXTA-FEIRA DIA 11/09/2020, DEPOIS SERÁ ENCERRADO... 

ATÉ TERÇA-FEIRA ÀS 7H15 MINUTOS 

ACESSAR O LINK DA CHAMADA DISPONÍVEL ATÉ O DIA 11/09/2020. 

LISTA DE CHAMADA 08/09/2020 - AULA DE FÍSICA - 3º ANO A, B e C

Um Forte Abraço 

Profª Renata Spinelli 

RECUPERAÇÃO DE FÍSICA: 1º e 2º BIMESTRES - 3º ANOS A, B e C - PERÍODO DA RECUPERAÇÃO: 09/09/2020 À 15/09/2020.

 Olá Queridos Alunos 

Está disponível a RECUPERAÇÃO PARA OS BIMESTRES ANTERIORES... Conteúdo estudado no CMSP: Campo Magnético - Corrente Elétrica e Campo Magnético da TERRA. 

ATENÇÃO: PARA RESPONDER O QUESTIONÁRIO QUE ESTÁ DISPONÍVEL NO LINK ABAIXO, VOCÊ PRECISA ASSISTIR AS VÍDEOS AULAS QUE ESTÃO "AQUI".... 

                                           AULA 1: 

                                            AULA 2:

ATENÇÃO O LINK PARA RECUPERAÇÃO FICARÁ DISPONÍVEL ATÉ O DIA 15/09/2020, APÓS ESSE PERÍODO, SERÁ ENCERRADO... 

POR GENTILEZA: O TRABALHO É INDIVIDUAL, ASSISTA AS VIDEOS AULAS ... E, ESCREVA O QUE VOCÊ ENTENDEU DAS AULAS... CÓPIAS DA INTERNET OU DE OUTROS MEIOS, NÃO SERÃO ACEITAS... 

LINK

 

TRABALHO DE RECUPERAÇÃO BIMESTRES ANTERIORES 1º e 2º BIMESTRES DE FÍSICA.

Um forte Abraço 

Profª Renata Spinelli 

E.E.LEDA - AULA DE FÍSICA: REVISÃO PARA O ENEM - 3º ANO A, B e C - DATA: 01/09/2020 - CONTEÚDO: INTRODUÇÃO DA NATUREZA DA ONDA

 Olá Queridos Alunos 

Hoje, começamos a nossa revisão para o ENEM, serão três aulas Estudando o COMPORTAMENTO DA ONDA - PROPAGAÇÃO - NATUREZA - VELOCIDADE E  COMPORTAMENTO... 

SEGUE O LINK DA CHAMADA DE HOJE, DISPONÍVEL ATÉ QUINTA-FEIRA: 03/09/2020. 

LISTA DE CHAMADA - ASSISTA AULA PARA RESPONDER AS PERGUNTAS QUE ESTÃO NA LISTA, CASO CONTRÁRIO SUA RESPOSTA NÃO SERÁ ACEITA, ISSO TAMBÉM VALE PARA CÓPIAS.

AVALIAÇÃO PARA O 3º BIMESTRE (NOTA):SUA PRESENÇA E  LISTA DE CHAMADA, COM A PERGUNTAS  REFERENTE A AULA. 

                                            

Assistir a aula de Hoje: 01/09/2020

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA - AULA DE FÍSICA: 2º ANO A, B e C - LISTA DE CHAMADA E ENTREGA DE ATIVIDADE - "ONDAS" - DATA 31/08/2020

 Olá Queridos Alunos 

Estamos Estudando a Natureza da Onda: Comprimento; Frequência; Amplitude e Período... 

Segue a Link da Aula de Hoje:

Acessar o LINK, abaixo: Lembrando que os Exercícios do Livro Deverão ser Feitos no Link da Chamada. Com todos os Processos de Cálculo e Dúvidas. Data para Entrega 05/09/2020...Dia 07/09/2020 não teremos aula "FERIADO"... 

AULA 31/08/2020 - LISTA DE CHAMADA E ATIVIDADE

Um Forte Abraço 

Profª Renata Spinelli 

EE Leda - 3º ano A, B e C - Física: Aula de Física - Revisão Enem.

 Olá Querido Alunos

O conteúdo de "Ondulatória" sempre cai nos Vestibulares e Enem... Assistam a vídeo aula abaixo... Não esqueçam de responder a lista de chamada. 

                                               Assista a aula... 

Lista de Chamada... Acessar o Link

Lista de Chamada - 20/08/2020. Revisão Enem

Um Forte Abraço

Profª Renata Spinelli 

EE LEDA - 2º anoa A, B e C - LISTA DE CHAMADA - Data: 20/08/2020. Introdução: Ondas.

 Olá  Queridos Alunos

 

Segue a Lista da Chamada da Aula de Hoje!!! Quem não conseguiu assistir a aula hoje, poderá assistir a aula e responder a Lista de Chamada... 

                                                         Aula de Hoje! Assistir... 

Acessar o Link. 

Lista de Chamada - 20/08/2020

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA - LISTA DE CHAMADA - 2º ANO A,B e C - FÍSICA

     Olá Queridos Alunos 

Segue a Lista de Chamada... Disponível até as 14h... 

acessar o Link Abaixo.

https://forms.gle/Up9bp1Wua11qn5ex8

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA - 9º ANO A, B e C - "EQUAÇÃO DO SEGUNDO GRAU - CMSP: AULA DIA 03/08/2020

Olá Queridos Alunos - 3º Bimestre/2020

Hoje, estudamos as "Equações do Segundo" - Usamos a Fórmula de Bháskara... 

                                             Aula do Dia 03/08/2020 - Equação do 2º Grau. 

Aula 27/07/2020 - Retomada Radiciação 

Não Esqueçam de Fazer a Lição no Caderno, com Todos os Processos de Cálculo (LIVRO DIDÁTICO DE MATEMÁTICA)

Um Forte Abraço 

Profª Renata Spinelli

E.E. LEDA - 2º ANOS A, B e C - AULÃO DE FÍSICA - ESTUDO DOS GASES - EQUAÇÃO DE UM GÁS IDELA

Olá Queridos Alunos 

ENCERRAMENTO DO 2º BIMESTRE

Segue a link  do "aulão de hoje"... O LINK SERÁ ENCERRADO AS 8H DA MANHÃ DO DIA 04/08/2020.... 

https://forms.gle/qp9xQzapk99jEbbR9

                                            AULÃO DE FÍSICA (ASSISTIR) - 03/08/2020 - 

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA: 2º ANO A, B e C - "FÍSICA " - EQUAÇÃO GERAL DE GASES .

Olá Queridos Alunos 

Quem não teve a oportunidade de assistir a aula, ontem poderá assistir... Agora!!! Façam as suas anotações... 

                                              Aula dia 15/07/2020

Um Forte Abraço 

Profª Renata Spinelli

EE LEDA - 3º ANOS A, B e C: FORAÇA MAGNÉTICA - MOTOR ELÉTRICO - LISTA DE CHAMADA

Olá Queridos Alunos


Segue o Link da Lista de Chamada - Veja a postagem anterior com a videoaula e assista a aula do CMSP, que está disponível no Cana do YouTube.

LISTA DE CHAMADA - SEMANA 16/07/2020

Um Forte Abraço

Profª Renata Spinelli

E.E LEDA - 3º ANO A, B e C: FÍSICA - FORÇA MAGNÉTICA - INTENSIDADE...

Olá Querido Alunos

Hoje, aprendemos a calcular a intensidade da "Força Magnética" no Campo Magnético...

                                            

Assistam a videoaula do dia 14/07/2020: Anotem todas as observações feitas - inclusive o Exercício Resolvido!

Na quinta-feira, será disponibilizado um Link - para lista de chamada! 

Um Forte Abraço 

Profª Renata Spinelli 

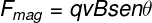
EE LEDA - 2º A, B e C - FÍSICA - LISTA DE CHAMADA E AULA ON LINE

Olá Queridos Alunos

Assistam a videoaula abaixo, da nossa última aula: 

Acessar o Link, abaixo da Chamada 

LISTA DE CHAMADA - SEMANA 16/07

NOSSA PRÓXIMA AULA SERÁ DIA 15/07/2020  - ÀS 13h15 min.... Com correção de Exercícios Envolvendo a Equação Geral dos Gases

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA - 9º ANO: MATEMÁTICA - SEMANA 06/07/2020 A 10/07/202 - CMSP

Olá Queridos Alunos

Estamos Estudando: Expressões Algébricas; Produto Notável e Equação do Segundo Grau.

Assistam, as aulas  da Semana Passada! Anotem todos os Exercícios no Caderno, não esqueçam de assistir as aulas do CMSP...

Aula do dia: 10/07/2020

Aula do dia: 08/07/2020

Aula do dia: 07/07/2020

Aula do dia: 06/07/2020

Novamente "assistam" às videoaula - no caderno anotem as datas, com os exercícios resolvidos em cada aula... 

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA - 2º A, B e C - FÍSICA -AULA: 09/07/2020: TRANSFORMAÇÕES DOS GASES

Olá Queridos Alunos 

Estou disponibilizando a aula de ontem... Assistam, façam anotações! Na Segunda teremos uma atividade 

Teórica. 

Na quarta-feira às 13h15 min. Na aula vamos resolver alguns exercícios, utilizando a equação geral dos Gases... 

                                            Aula 08/07/2020

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA - 3º ANO A, B e C: FÍSICA - CAMPO MAGNÉTICO: O GRANDE IMÃ...

Olá Queridos Alunos

Olá Queridos Alunos 

ESTAMOS, ESTUDANDO "CAMPO MAGNÉTICO"... VAMOS CONTINUAR "APRENDENDO SEMPRE".. 

NA QUINTA-FEIRA - SERÁ DISPONILIZADO UM LINK, DE CHAMADA E UMA PERGUNTA REFERENTE A AULA... 

AULA: 07/07/2020 - CARGA MAGNÉTICA.

Um Forte Abraço 

Profª Renata Spinelli 

EE LEDA - 9º ANO A, B e C - MATEMÁTICA - SEMANA DE ENTREGA DO TRABALHO.

Olá Queridos Alunos

Essa semana vamos estudar "Bastante": Teremos aulas nos seguintes dias:

Segunda-feira: 06/07/2020 - Horário: 18h às 18h45 min;
Terça-feira: 07/07/2020 - Horário: 17h15 às 18h45min;
Quinta-feira: 09/07/2020 - Horário: 18h às 18h45min;
Sexta-feira: 10/07/2020- Horário: 17h15min às 18h00 min.

Pessoal, pode acontecer uma alteração no Horário - mais mando no GRUPO:

ACESSAR O LINK DO TRABALH "ABAIXO": ATENÇÃO FAZER NO CADERNO TIRAR FOTO, ENVIAR PARA O E-MAIL: renataspinelli.leda@gmail.com

ATENÇÃO: USAR O LÁPIS COM GRÁFITE ESCURO - EXERCÍCIOS EM ORDEM, EM CASO DE DÚVIDAS, ANOTAR NO PRÓPRIO EXERCÍCIO...

ACESSAR O LINK "ABAIXO":

TRABALHO DE MATEMÁTICA - RADICIAÇÃO; EXPRESSÕES E EQUAÇÕES

CONTINUAÇÃO DO TRABALHO DE MATEMÁTICA - NOTAÇÃO CIENTIFICA E PROPRIEDADES

Acessar as aulas on-line:

                                          Aula 2: 30/06/2020

Aula 1: 26/06/2020. 

Aula: 24/06/2020 - Propriedades dos Radicais.

Um Forte Abraço 

Profª Renata Spinelli 

2º ANOS A, B e C - AULA DE FÍSICA: 01/07/2020 - CALOR LATENTE: ESTUDO DO GRÁFICO - MUDANÇA DE ESTADO FÍSICO.

Olá Queridos Alunos 

Na próxima semana,vamos estudar:

- Estudo dos Gases: Transformações gasosas (isotérmica; isométrica; isobárica); 

- Gás perfeito e gás real; 

- Uma pequena Introdução da Equação de Clapeyron e Constante de Avogadro.

Simulador phet - Comportamento dos Gases: 

Acessar:

https://phet.colorado.edu/sims/html/gas-properties/latest/gas-properties_pt_BR.html

Turma assistam a videoaula abaixo, e anotem as informações e conceitos:

Aula do dia 01/07/2020 - ACESSAR O LINK

https://www.youtube.com/watch?v=JZ5KWnhhPd4&feature=youtu.be

Um Forte Abraço 

Profª Renata Spinelli 

3º ano A, B e C - Aula Complementar CMSP - FÍSICA

Olá Queridos Alunos

Acessar o Link, abaixo:

AULA ON-LINE: INTRODUÇÃO AO CAMPO MAGNÉTICO.

                                             Experimento do Campo Magnético da Terra...

Façam as anotações, que considerar "importante"... E, Vamos Estudar!!!!

Um Forte Abraço

Profª Renata Spinelli  

9º ANO A, B e C - MATEMÁTICA: ROTEIRO DE AULAS AO VIVO E TRABALHO.

Olá Queridos Alunos

Segue o "ROTEIRO DE AULAS" do 2º Bimestre - Fiquem atentos as aulas...Sua participação será muito importante...

ROTEIRO DE MATEMÁTICA  – 2º BIMESTRE – TURMA: 9º ANO A, B e C

Profª Renata Spinelli e Profª Tereza

Conteúdo: Potenciação (notação científica); Radiciação – Propriedades; Produto Notável (quadrado perfeito) e Equação do Segundo Grau.

HABILIDADES: (EF09MAT18); (EF09MA03); (EF09MA04); (EF09MA09); (EF09MA06); (EF09MA22)

MATERIL DIDÁTICO:

CADERNO DO ALUNO: SP FAZ ESCOLA: MATEMÁTICA – VOL.2;

Livro Didático: A CONQUISTA DA MATEMÁTICA; José Ruy Giovanni Júnior; Benedicto Cadstrucci; Ed. FTD – ano: 2018. Material de Apoio – Diversos;

- E-mail: renataspinelli.leda@gmail.com (para entrega de trabalhos);

- WhatsApp (grupos das turmas: Dúvidas e Orientações)

DATAS:

06/07/2020 à 10/07/2020 – Entrega do Trabalho Bimestral;

Atenção: Não enviar nenhuma atividade de aprendizagem; No dia 06/07/2020,vou enviar o Trabalho de Entrega.

Avaliação de Aprendizagem Bimestral – 20/07/2020 à 24/07/2020 – Horário da aula, “Definir o dia da Semana”.

Aula ao Vivo – Correção Comentada e Explicação do Conteúdo.

TODAS AS TERÇAS-FEIRAS E SEXTAS-FEIRAS: HORÁRIO – 17H15 MIN AS 18H15MIN.

Qualquer alteração, Vocês serão comunicados pelo grupo do Whatshap. 

Um Forte Abraço 

Profª Renata Spinelli